Strain Energy Stored Due To Bending
Let’s assume a beam that is subjected to a uniform moment M. Consider an elemental length ds of the beam between two sections 1-1 and 2-2.
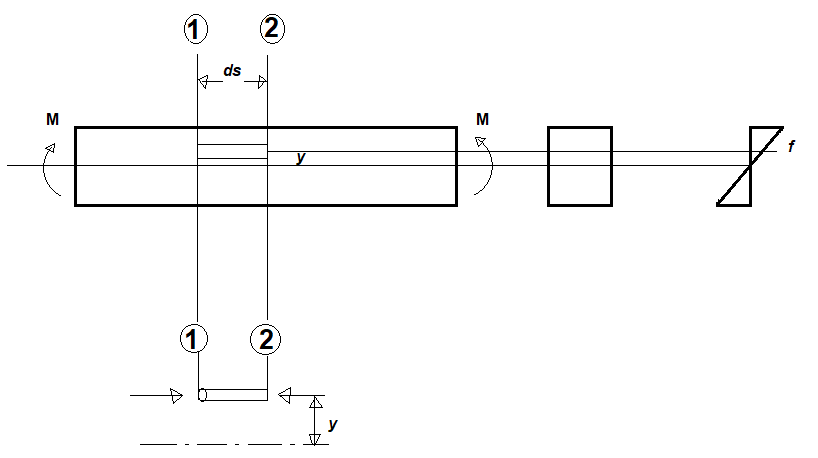
The elemental length of the beam may be assumed as consisting of an infinite number of element cylinders each of area da and length ds. Consider one such elemental cylinder located y units from the neutral layer between the section 1-1 and 2-2.
Now, the intensity of stress in the element cylinder = [latex] f = \frac{M}{I}y [/latex]
Where I = Moment of inertia of the entire section of the beam about the neutral axis.
So, Energy stored by the element cylinder = (Energy stored per unit volume⨯Volume of the cylinder)
= [latex] \frac{f^{2}}{2E}\cdot da\cdot ds [/latex]
= [latex] \frac{1}{2E}\left (f^{2} \right )da\cdot ds [/latex]
= [latex] \frac{1}{2E}\left ( \frac{M}{I}y \right )^{2}da\cdot ds [/latex]
= [latex] \frac{M^{2}}{2EI^{2}} ds\cdot da\cdot y^{2} [/latex]
Energy stored by ds length of the beam = Sum of the energy stored by each elemental cylinder.
Between the two sections 1-1 and 2-2.
= [latex] \sum \frac{M^{2}}{2EI^{2}} ds\cdot da\cdot y^{2} [/latex]
= [latex] \frac{M^{2}}{2EI^{2}} ds\cdot \sum da\cdot y^{2} [/latex]
But, ∑da.y2 = Moment of inertia of the beam section about the natural axis = I
So, The energy stored by the ‘ds‘ length of the beam
= [latex] \frac{M^{2}}{2EI^{2}} ds\cdot I [/latex]
= [latex] \frac{M^{2}}{2EI} ds [/latex]
And,
The total energy stored due to bending by the whole beam = [latex] \int \frac{M^{2}}{2EI} ds [/latex]