Bending of Rails on Curves
Curves of less than 3 degrees are considered to be flat curves and in this case, rails can be kept in curved position by sleepers which are maintained in place by the ballast.
The curvature greater than 3 degrees are considered to be a sharp curve. In order to correct the curvature, it is desirable to bend the rails.
Otherwise, the side thrust on ballast at the ends of the sleepers due to the rail which acts as a spring, that is sufficient to form elbows and disturb the alignment of the track.
The amount by which the rail is to be bent can be easily found out as shown in Fig.
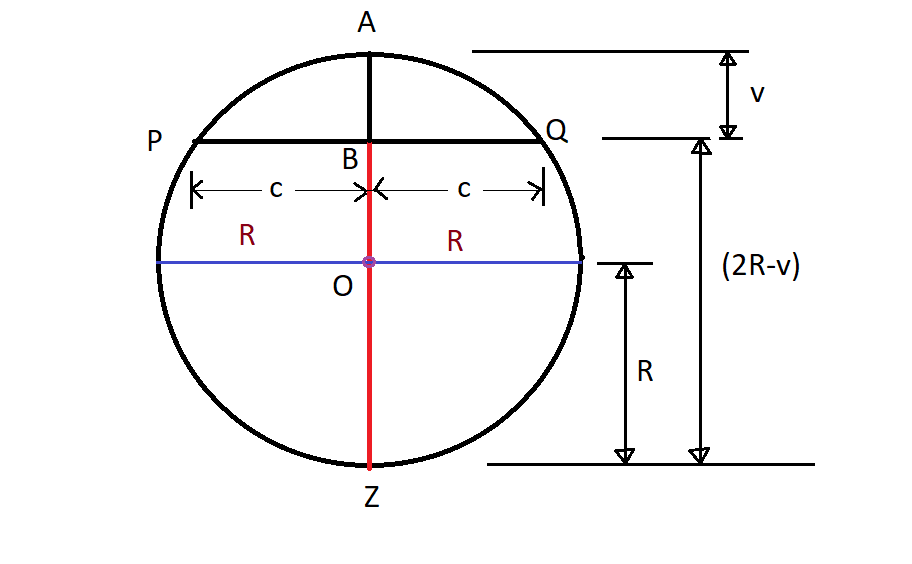
- AB = v = Rise of rail at center
- PB = BQ = c = One-half of the chord length
- R = Radius of the curve
Now we can write,
⇰ AB ☓ BZ = PB ☓ BQ
⇰ v ☓ (2R-v) = c ☓ c
⇰ 2Rv – v2 = c2
⇰ v = c2 / 2R [ Neglecting v2 , as this will be very small]
Mathematics Example:
Example: For a 12 m rail length to be laid on a 4 degree curvature
Solution: Here, 12 m rail length means the total length of the chord. So, the value of c will be 6 m ( c = One-half of the chord length).
v = c2 / 2R
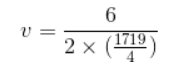
Where, R = (1719/4)
v = 0.0418 m = 4.18 cm = 42 mm (approximately)
Read More: