Capillarity Permeability Test
In the previous articles, We have discussed Falling Head Permeameter and Constant Head Permeameter for the determination of the coefficient of permeability of the soil. In this article, we are going to discuss the capillarity permeability test or the horizontal capillarity test, which is another method used for determining the coefficient of permeability as well as the value of the capillarity height of the soil sample.
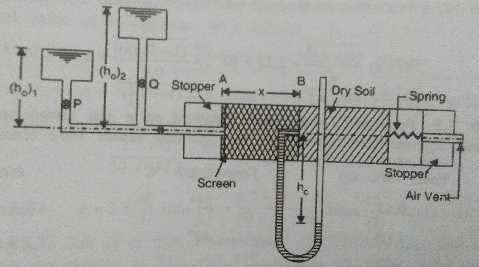
In this test, a sample of dry soil, at the desired density is placed in a transparent glass or lucite tube, about 4cm in diameter and 35 cm long. Water is allowed to flow through the soil sample from one end, under a constant head [latex] h_0 [/latex] and the other end is kept open to the atmosphere through an air vent tube.
At any time interval ‘t’ after the beginning of the test, let the capillary water travels through a distance x from point A to B. At the point A, there is a pressure head [latex] h_0 [/latex], while at the point B, there is a pressure deficiency [latex] h_c [/latex] ( i.e., a negative pressure head ).
Head lost in causing flow from A to B (x distance apart)
[latex] = h_{0} - (-h_{c}) = h_{0} + h_{c} [/latex]
Hydraulic gradient
[latex] i = \frac{h_{0} + h_{c}}{x} [/latex]
From Darcy's law
[latex] v = K.i [/latex] [Where [latex] v_{s} = \frac{v}{n} [/latex] ]
Or, [latex] n.v _{s} = K.i [/latex]
Where [latex] v [/latex] = Discharge velocity,
[latex] v_{s} [/latex] = Seepage velocity
and [latex] n [/latex] = Porosity
But seepage velocity = [latex] \frac{dx}{dt} [/latex]
If the coefficient of permeability is designated as [latex] K_u [/latex] at a partial saturation [latex] S [/latex], then the above expression may be rewritten as:
[latex] S.n.v_{s} = K_{u}.i [/latex]
[latex] S.n. \frac{dx}{dt} = K_{u}. \frac{h_{0} + h_{c}}{x} [/latex]
Or, [latex] x.dx = \frac{K_{u}}{S.n} (h_{0} +h_{c}) . dt [/latex]
Integrating between the limit [latex] x_1 [/latex] and [latex] x_2 [/latex] for [latex] x [/latex], and corresponding values of time [latex] t_1 [/latex] and [latex] t_2 [/latex], we get
[latex] \int_{x_{1}}^{x_{2}} x.dx = \frac{K_{u}}{S.n}(h_{0}+h_{c})\int_{t_{1}}^{t_{2}} dt [/latex]
[latex] \left |\frac{x^2}{2} \right |_{x_1}^{x_2} = \frac{K_{u}}{S.n} (h_{0}+h_{c})\left |t \right |_{t_1}^{t_2} [/latex]
[latex] \frac{(x_{2}^{2} - x_{1}^{2})}{(t_{2} - t_{1})} = \frac{2K_{u}}{S.n} (h_{0}+h_{c}) [/latex]
If [latex] S [/latex]= 100% ( that means S= 1). Now, the above expression becomes
[latex] \frac{(x_{2}^{2} - x_{1}^{2})}{(t_{2} - t_{1})} = \frac{2K_{u}}{n} (h_{0}+h_{c}) [/latex]
In the above equation, there are two unknowns: [latex] k [/latex] and [latex] h_c [/latex]. In order to overcome this difficulty, the test is performed in two stages, with two different heads of water [latex] h_0 [/latex]. The first set of observations is taken under a head [latex] h_{(0)1} [/latex] up to capillary saturation penetrating about half the length of the test tube.
As the capillarity saturation proceeds, the value of [latex] x [/latex] is recorded at various time intervals. A graph between [latex] x^2 [/latex] and [latex] t [/latex] will give a straight line, and its slope is given as:
[latex] \frac{(x_{2}^{2} - x_{1}^{2})}{(t_{2} - t_{1})} = m_1 [/latex]
In the second stage, for the next half of the tube, is performed with head [latex] h_{(0)2} [/latex], and the recorded values of x and t are again used to plot a graph between [latex] x^2 [/latex] and [latex] t [/latex]. The slope of this line, say [latex] m_2 [/latex], is now determined.
[latex] \frac{(x_{2}^{2} - x_{1}^{2})}{(t_{2} - t_{1})} = m_2 [/latex]
Knowing the two slopes, the values of [latex] h_0 [/latex] and [latex] k [/latex]can be computed by the following two-equation.
[latex] \frac{(x_{2}^{2} – x_{1}^{2})}{(t_{2} – t_{1})} = m_1 = \frac{2K_{u}}{S.n} (h_{0(1)}+h_{c}) [/latex]
[latex]\frac{(x_{2}^{2} – x_{1}^{2})}{(t_{2} – t_{1})} = m_2 = \frac{2K_{u}}{S.n} (h_{0(2)}+h_{c})[/latex]
The degree of saturation S can also be found by measuring the wet mass of the soil sample at the end of the experiment. The porosity is computed from the known dry mass, volume and specific gravity.
Read More:
Factors Affecting The Permeability