Switch Angle in Railway
Switch angle or angle of switch divergence is defined as the angle formed between the gauge lines of the stock rail and tongue rail(Switch rails).
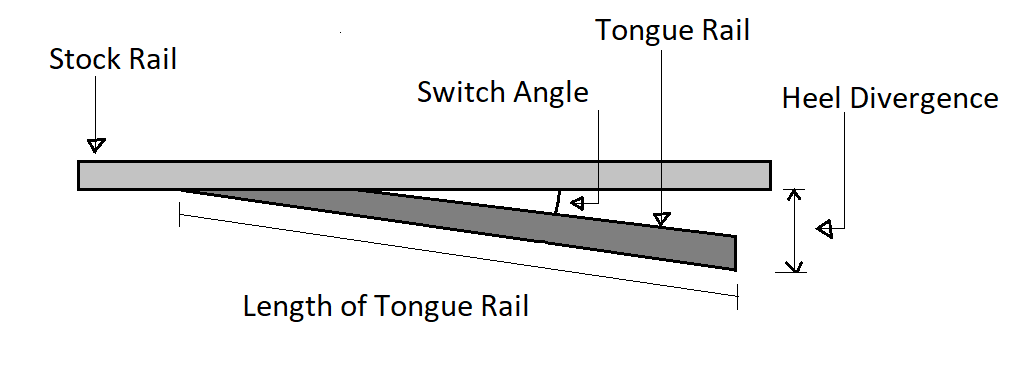
If the switch angle is more, the entry of the train will not be smooth and consequently, the speed of the train will have to be reduced. On the other hand, a small switch angle will increase the overall length of the turnout.
Hence, small switch angles are provided in the case of fast-moving trains. But, in the case of slow-moving trains or station yards, a greater switch angle is recommended.
The switch angle depends on the length of tongue rails and heel divergence, which is given below:
Case:1 When the thickness of tongue rails at toe = 0
Let,
- d = Heel divergence
- D = Length of tongue rail
- [latex] \theta [/latex] = Switch Angle
Now, from the above Fig.
[latex] \sin \theta [/latex] = (heel divergence / Length of tongue rail) = [latex] \frac{d}{D} [/latex]
Switch Angle = [latex] \theta [/latex] = [latex] \sin ^{-1}\frac{d}{D} [/latex]
Case:2 When the thickness of tongue rails at toe = t

Let,
- t = Thickness of tongue rail at toe
- [latex] D_{1} [/latex] = Actual length of tongue rail
- [latex] D_{2} [/latex] = Theoretical length of tongue rail
- x = Difference between [latex] D_{1} [/latex] and [latex] D_{2} [/latex]
From the above equation and fig, we can write
- Actual Length of tongue rails [latex] D_{1} [/latex]= [latex] \frac{ ( d – t ) }{ \sin \theta } [/latex]
- Theoretical Length of tongue rails [latex] D_{2} [/latex] = [latex] \frac{d}{ \sin \theta } [/latex]
Now, x = ( [latex] D_{2} [/latex] – [latex] D_{1} [/latex] ) = [latex] \frac{t}{ \sin \theta } [/latex]
Read More: