Swedish Circle Method
Swedish circle method for analyzing the slope stability:
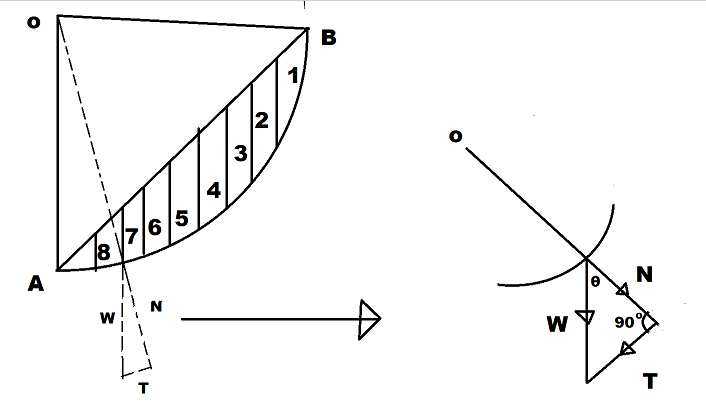
This method was first introduced by Fellenius (1926) for the analysis of slope stability of C-φ soil. In this method, the soil mass above the assumed slip circle is divided into a number of vertical slices of equal width. The forces between the slices are neglected and each slice is considered to be an independent column of soil of unit thickness. The location of the center of the failure arc (o) is assumed.
The weight of slice [latex] (w) = \gamma bh [/latex]
Where,
- [latex] \gamma [/latex] = Bulk unit weight of soil;
- h = Average height of slice &
- b = Width of slice.
The weight of each slice (w) is plotted as a vector and it passes through the midpoint of each slice and is divided into normal & tangential components N & T respectively.
Then,
- N=W cosα
- T=W sinα
Considering the whole slip surface AB of length ‘L’. If ‘c’ is the unit cohesion, then the resisting force, from Coulomb’s equation is equal to (c L + N tanφ’):
Now,
Driving force = ΣT
Resisting force =c L + tanφ’ ΣN
Driving moment =(ΣT) × R
Resisting moment = c L R+ (tanφ’ ΣN × R).
- ΣT = Sum of all tangential components.
- ΣN = Sum of all normal components.
So, the Factor of safety (FOS) against sliding is
[latex] F =\frac{Resisting Moment}{Driving Moment}= \frac{c L + \tan \phi \sum N}{\sum T} [/latex]
Putting, N=W cosα, and T=W sinα
[latex] F = = \frac{c L + \tan \phi \sum W \cos \alpha }{\sum W \sin \alpha } [/latex]
Read More:
Assumption of Coulomb’s Theory