How to Calculate Weight of Steel Bar Used in RCC Structure
There are two ways to calculate the weight of the steel bar used in RCC work. You can calculate the weight either using the formula or following the general procedure. The formula will help you to get quick results. So, it will save your time. But the general way will help you to know the exact way of calculation.
Calculate the Weight of the Steel bar by Using Formula
The weight of the steel bar can be calculated by using the (d2 ÷ 162) formula, where ‘d’ is the dia of a bar in mm.
Example 1: Let’s assume the dia of a bar is 12 mm.
So, the weight of the bar will be = (122 ÷ 162) = 0.888 kg/m.
Example 2: Let’s assume the dia of a bar is 12 mm and the length is 3 m.
So, the weight of bar will be = (122 ÷ 162) × 3 = 0.888 × 3 = 2.664 kg.
Example 3: Let’s assume the dia of a bar is 16 mm and the length is 4.5 m.
Therefore, the weight of bar will be = (162 ÷ 162) × 4.5 = 1.58 × 4.5 = 7.11 kg.
Example 4: Let’s assume the dia of a bar is 20 mm and the length is 10 ft.
The length of the bar is given in feet. So, we need to convert it in a meter. 10 ft = 3.048 m. [Note: 1ft = 0.3048 m]
The weight of the bar will be = (202 ÷ 162) × 3.048 = 2.469 × 3.048 = 7.52 kg
Weight of Steel bar Per Meter Length for Different Dia of Bar
| Dia of bar | Calculation | Weight per meter |
| 6 mm | (62 ÷ 162) | 0.222 kg/m |
| 8 mm | (82 ÷ 162) | 0.395 kg/m |
| 10 mm | (102 ÷ 162) | 0.617 kg/m |
| 12 mm | (122 ÷ 162) | 0.888 kg/m |
| 16 mm | (162 ÷ 162) | 1.58 kg/m |
| 20 mm | (202 ÷ 162) | 2.469 kg/m |
| 25 mm | (252 ÷ 162) | 3.858 kg/m |
| 28 mm | (282 ÷ 162) | 4.839 kg/m |
| 32 mm | (322 ÷ 162) | 6.32 kg/m |
| 36 mm | (362 ÷ 162) | 8 kg/m |
| 40 mm | (402 ÷ 162) | 9.876 kg/m |
Calculate the Weight of the Bar by Following General Procedure:
In this method, we need to calculate the volume of the bar. We know, a steel bar that looks like a solid cylinder
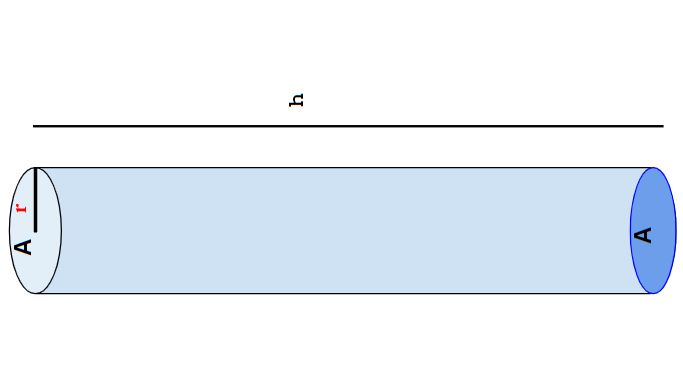
The volume of the steel bar(V) = A × h = πr2 × h.
Where ‘A’ is the area of the base, ‘h’ is the height/length of the bar, and r is the radius of the bar. [ r = d/2, where, ‘d’ is the dia of the bar].
We know, the density of the bar is (γ) = 7850 kg/m3
Therefore, the weight of steel bar = Volume of the bar × Density of bar = πr2h × γ.
Example 1: Let’s assume the dia of a bar is 8 mm, and the length is 3 m.
- r = d/2 = 8/2 = 4 mm.
- h = 3 m.
- A = πr2 = π(4)2 = 50.26 mm2 = 5.026 × 10-5 m2.
- V = A × h = 5.026 × 10-5 × 3 = 1.507 × 10-4 m3.
The weight of the bar = V × γ = 1.507 × 10-4 × 7850 =1.18 kg.
Example 2: Let’s assume the dia of the bar is 12 mm and the length is 3 m.
- r = d/2 = 12/2 = 6 mm.
- h = 3 m.
- A = πr2 = π(6)2 = 113.097 mm2 = 1.1309 × 10-4 m2.
- V = A × h = 1.1309 × 10-4 × 3 = 3.3929 × 10-4 m3.
The weight of the bar = V × γ = 3.3929 × 10-4 × 7850 = 2.66 kg.
Read More:
How to Calculate Quantity of Cement, Sand & Aggregate in M20