Relation Between Dry Unit Weight, Specific Gravity, Percentage of Air Voids, and Water Content
In this article, we shall make the formula or relation between the dry unit weight([latex]\gamma _{d}[/latex]), specific gravity(G), percentage of air voids, and water content(w).
[Note: Dry unit weight means dry density]
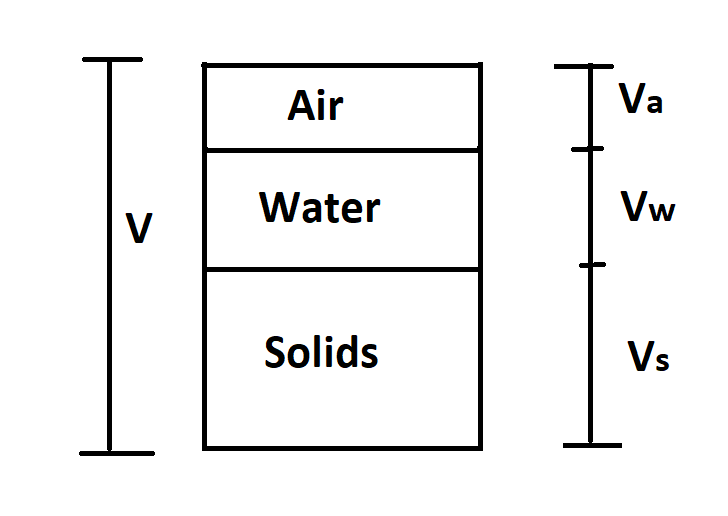
Soil three-phase diagram is shown in the above picture. From this diagram, we can write,
Total Volume = Volume of solids ([latex] V_{s} [/latex])+ Volume of water ([latex] V_{w} [/latex]) + Volume of air ([latex] V_{a} [/latex])
[latex]V = V_{s} + V_{w} + V_{a}[/latex]
[Both sides divided by V]
Or, [latex]\frac{V}{V}= \frac{V_{s}}{V} + \frac{V_{w}}{V} + \frac{V_{a}}{V}[/latex]
[We know, [latex] \frac{V_{a}}{V} = n_{a} [/latex]]
Or, [latex]1 = \frac{V_{s}}{V} + \frac{V_{w}}{V} + n_{a}[/latex]
Or, [latex]1 – n_{a} = \frac{V_{s}}{V} + \frac{V_{w}}{V}[/latex]
[ We know, [latex] \gamma_{s} = \frac{W_{s}}{V_{s}} [/latex], and Specific Gravity(G) [latex] = \frac{\gamma_{s}}{\gamma_{w} } = \frac{W_{s}}{V_{s}\gamma_{w} }[/latex] ]
[From this equation, [latex]G = \frac{W_{s}}{V_{s}\gamma_{w} }[/latex], we can write [latex] V_{s} = \frac{W_{s}}{G\gamma _{w}} [/latex]. Now, place the value of [latex] V_{s} [/latex] in the above equation.]
Or, [latex]1 – n_{a} = \frac{W_{s}/G\gamma_{w}}{V} + \frac{W_{w}/\gamma _{w}}{V}[/latex]
[We know, Density of solids[latex](\gamma_{d}) = \frac{W_{s}}{V}[/latex]]
Or, [latex]1 – n_{a} = \frac{\gamma_{d}}{G\gamma_{w} } + \frac{wW_{s}/\gamma _{w}}{V}[/latex]
Or, [latex]1 – n_{a} = \frac{\gamma_{d}}{G\gamma_{w} } + \frac{w\gamma_{d} }{\gamma_{w} }[/latex]
Or, [latex]1 – n_{a} = \frac{\gamma_{d}}{\gamma_{w} }\left [ w + \frac{1}{G} \right ] [/latex]
[latex]\gamma_{d} = \frac{(1 – n_{a})G \gamma_{w}}{1 + wG}[/latex]
Read More:
Relation Between Dry unit Weight, Bulk unit Weight & Water Content
Relation Between Void Ratio, Water Content, Degree of Saturation & Specific Gravity